BOSKE

 PITAGORINA TEOREMA

Pitagorina teorema glasi:

Zbir površina kvadrata konstruisanih nad katetama kao stranicama  jednak je povrini kvadrata konstruisanog nad hipotenuzom kao stranicom.

ili jednostavnije:

Kvadrat nad hipotenuzom jednak je zbiru kvadrata nad obe katete

 

 

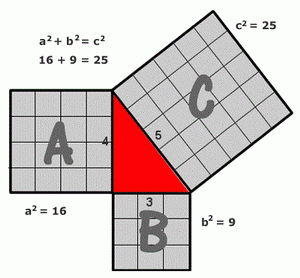
  Pitagorina teorema kod geometrijskih fgigura

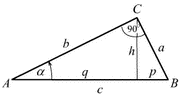
Pravolugli trougao

Dve stranice trougla zaklapaju prav ugao i nazivaju se katete. Stranica naspram pravog ugla je hipotenuza i ona je najveća stranica ovog trougla.

c² = a² + b²

c - hipotenuza

a, b - katete

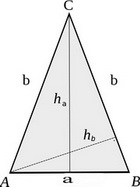
Jednakokraki trougao:

Jednakokraki trougao ima jednake krake. Visina na osnovicu pada pod pravim uglom na njenu polovinu. Krak trougla, polovina osnovice i visina na osnovicu obrazuju pravougli trougao.

 b² = (a /2)² + ha²

ha - visina povučena na osnovicu jednakokrakog trougla

a - osnovica jednakokrakog trougla

b - krak  jednakokrakog trougla

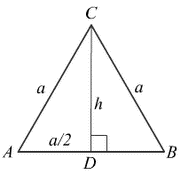
Jednakstranični trougao 

Jednakostranični trougao ima sve jednake stranice (kraci su jednaki osnovici) i jednake uglove od 60⁰. Visina sa osnovicom gradi prav uga i polovi je. Krak trougla, polovina osnovice i visina na osnovicu obrazuju pravougli trougao.

 a² = (a /2)² + ha²

ha - visina povučena na osnovicu jednakostraničnog trougla

a - osnovica, odnosno krak jednakostrančnog trougla

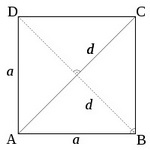
Kvadrat

Kvadrat ima sve jednake stranice i jednake uglove od 90⁰. Dijagonale kvadrate su jednake i seku se pod pravim uglom. Stranice kvadrata i njegova dijagonala obrazuju pravougli trougao.

 d² = a² + a²

d- dijagonala kvadrata

a - osnovica kvadrata

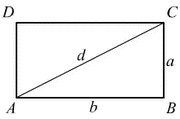
Pravougaonik

Pravougaonik ima po dve jednake stranice i sve jednake uglove od 90⁰.  Osnovice pravougaonika zaklapaju prav ugao i sa dijagonalom obrazuju  pravougli trougao.

 d² = a² + b²

d - dijagonala  pravougaonika

a - duža osnovica pravougaonika

b - kraća osnovica pravougaonika

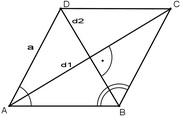
Romb

Romb ima sve jednake stranice i po dva jednaka ugla. Dijagonale romba seku se pod pravim uglom. Polovine dijagonala romba i stranica romba obrazuju pravougli trougao.

 a² = (d₁/2)² + (d₂ /2)²

a - osnovica romba

d₁ - duža dijagonala romba

d₂ - kraća dijagonala romba

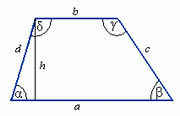
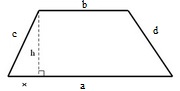
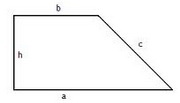
Trapez

Osnovice trapeza su paralelne. Visina trapeza povučena iz krajeva manje osnovice zaklapaju sa većom osnovicom prav ugao i odsecaju na njoj odsečke x i y.  Visina, odsečak i odgovarajući krak trapeza obrazuju pravougli trougao.

 c² = x² +  h²    ili     d² = y² +  h²

c, d - kraci trapeza

x, y - odsečci na većoj osnovici trapeza

h - visina trapeza                 

a, b   -  osnovice trapeza

Jednakokraki trapez:

Kod jednakokrakog trapeza kraci su jednaki (c=d), kao i odsečci na većoj osnovici trapeza (x  = y). Odsečak x je jednak polovini razlike veće i manje osnovice trapeza:

 x = (a - b)/2

Pravougli trapez:

Kod pravouglog  trapeza jedan krak je jednak visini trapeza, a odsečak x je jednak razlici veće i manje osnovice trapeza:

 x = a - b