BOSKE

 MNOGOUGAO

Mnogougao je deo ravni koji je ograničen zatvorenom izlomljenom krivom linijom.

 

 

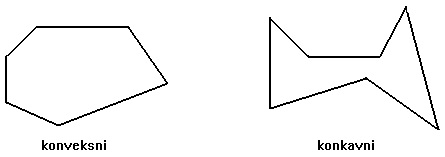
Mnogougao može da bude konveksni i nekonveksni (konkavni) mnogougao. Konveksi mnogougao je mnogougao kod koga duž koja spaja dve tačke izlomljene linije ne seče nijednu njegovu stranicu. Ako duž koja spaja dve tačke izlomljene linije seče stranicu mnogugla tada je taj mnogougao nekonveksni ili konkavni mnogougao.

 

  Obrasci

Za svaki mnogougao važi sledeći obrasci:

1) Zbir unutrašnjih uglova mnogougla Sn

Sn = (n - 2) 180^o

n -  broj stranica (broj unutrašnjih uglova, broj temena mnogougla)

2) Ukupan broj dijagonala mnogougla Dn

Dn = n (n - 3) / 2

3) Broj dijagonala iz jednog tjemena mnogugla dn

Dn = (n - 3)

4) Zbir spoljašnjih uglova mnogougla je 360^o

 

  Pravilni mnogougao

Mnogougao je pravilan ako su mu sve stranice i svi unutrašnji uglovi medjusobno podudarni. Za svaki pravilni mnogougao važi sledeće:

1)  Pravilni mnogougao je osnosimetrična figura sa n osa simetrije.

2)  Ako je broj stranica n paran, onda je on centralno simetričan.

3)  U pravilni mnogougao se može upisati kružnica i oko njega  opisati kružnica.

4)  Centar opisane i centar upisane kružnice mnogougla se poklapaju.

5)  Svi unutrašnji uglovi pravilnog mnogougla su jednaki i iznose:

α = Sn / n     

(α₁ + α₂ + α₃ + ....+ α_n = Sn)

6)  Svi spoljašnji uglovi pravilnog mnogougla su jednaki i iznose:

 α ₁ = 360^o / n   

6)  Zbir unutrašnjeg i spoljašnjeg ugla pravilnog mnogougla jednak je opružnom uglu.

 α + α₁ = 180^o

8) Obim pravilnog mnogougla je

O = a^.n   

a - dužina stranice

9) Površina pravilnog mnogougla

P = n  P∆ 

P∆ = a^.h / 2  - površina karakterističnog trougla mnogougla)

10) Centralni ugao pravilnog mnogougla

φ = 360^o / n